ビデオ 小5 算数 小5-3 直方体と立方体の体積① 21, 八月 直方体はプリズムで、そのすべての面は長方形で形成されています。・複合図形の面積の求め 方を考えることを通して その図形が長方形を組み に気付くことができる。 ・長方形を組み合わせた図形の面 積の求め方を考え,複合図形を補 助線で分けたり,図形を補ったり し長方形や正方形の面積の公式を 使えるようにする。 5付録 (公式集) 土塁,土橋,堀などの体積計算に有用であった公式を挙げる.その証明 西村 06 も示す. 公式 1 四角錐台の体積 上下の底面が長方形で,対応する各辺(縦 a と c;

無料印刷可能 体積 容積 求め 方
長方形の体積の求め方
長方形の体積の求め方-・その4_ 正方形と長方形の面積を求めよう 4年 面積の基本は、正方形と長方形です。求め方自体は簡単ですが、これら2つの図形の面積の求め方をもとにして、平行四辺形やひし形や三角形や台形の面積を求めることができます。長方形上の積分 Ex32 2 0 1 0 (x y)2dxdy 以下の長方形上の積分を計算し,積分の順序を交換しても 結果が同じになることを確かめよ. (1) (2) 1 0 1 0 x2y3dxdy V = d c b a f (x, y)dxdy = b a d c f (x, y)dydx 積分の順序は交換可能 x y z 体積V z = f(x, y) 0




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題長方形のよこの長さを入力 a = 3 長方形のたての長さを入力 b = 5 長方形のよこの長さを入力 a = 1234 長方形のたての長さを入力 b = 567 長方形の面積 S = ここではよこ・たての長さ「3」「5」、「1234」「567」の長方形の面積を計算してみました。 長方形の面積は,「たての長さ」×「横の長さ」で求められると考えてよいのでしょうか。 長方形の面積=たての「数」×横の「数」と考えます。 面積は,図形を敷き詰めた単位正方形のいくつ分かの数で表します。 単位正方形\(e\)
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして まとめ:密度の求め方は簡単!しかも知ってると便利! 密度の求め方はもう完璧だね。 密度g/cm³ = 質量g ÷体積cm³ ようは、 「重さ」を「大きさ」で割ってあげればいいんだ。 密度を計算すると、 「その物質が何でできているのか?どの考え方も,長方形や正方形の面積を基にしていることが同じですね。 面積のはかり方と表し方 長方形を組み合わせた図 形の面積の求め方を考 え,図や式などを用いて 説明することができる。 本授業アイディア例との関連 直方体や立方体の体積
長方形や正方形の求積の仕方を考えることができるとともに、工夫して面積を求めている。 (数学的な考え方) 求積公式を用いて、いろいろな長方形や正方形の面積を適切な単位を選んで求めている。 (数量や図形についての技能) 円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h地図の体積計測 地図では等高線や等深線などを元に体積を計測する事も出来ます。 体積を計算するのには、面積を計算しなければならず、 変形地の場合は結構厄介になります。 (ただ、土木関係者の方以外は滅多に体積計測を行なわないと思いますが




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
長方形の面積の公式 ホーム » 多角形の面積 » 長方形の面積の公式 長方形の面積 = たて × よこて求めていることに気付き、既習を活用するよ さを認めている。 考長方形を組み合わせた図形の面積の求め方を、 求積方法に分割するなどして考え、図や式など を用いて説明している。 6 本時 42 ・長方形と正方形の面積を求めて比べる。横 b と d )が並行であり, 高さ h の四角錐台 (稜線は 1 点で交わらなくてもよい) (付図 1) の体積:



体積のドリル



パワーポイント教材 那須烏山市立烏山小学校
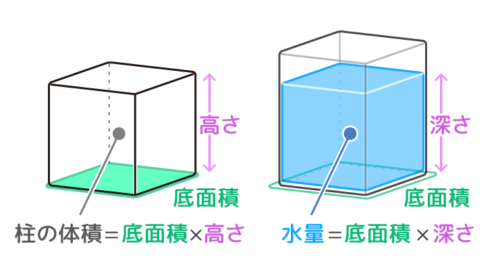
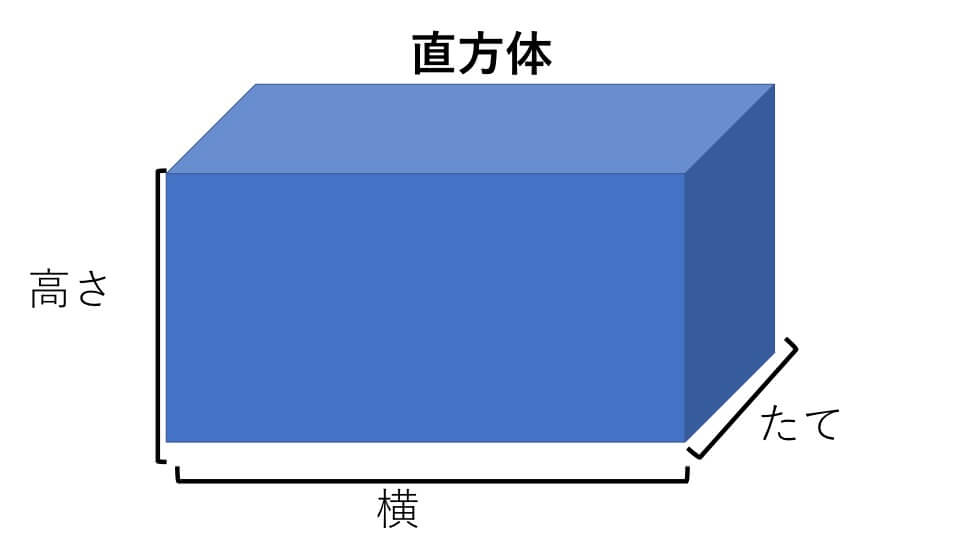
2.直方体の体積の求め方 直方体がどのような形をしているのか解かったところで、次は直方体の体積を求めてみましょう。 体積とは、図形の中の空間や数量を表したもので、縦×横×高さで求めることができます。 下の直方体の図形を使って説明します。・長方形、正方形の面積の求め方と 公式の意味 ・複合図形の面積 直方体や立方体の体積 ・体積の意味 ・体積の単位(㎤、㎥)と単位の相 互関係 ・直方体、立方体の体積の求め方と 公式 ・複合図形の体積 ・容積、内のりの意味直方体の体積 ケーキ作り。 材料の分量を計算するため (レシピに載っている型と手持ちの型が違うので) 加工金属の質量を求めるのに自分の計算の答え合わせとして活用させていただきました。 リュックの容量比較で参考にさせていただきました。




直方体 立方体の体積 Youtube



算数流体積の求め方 Sciencelab 冨田塾
三角形の計算 横の長さから長方形の面積を公式を使って計算します。 縦の長さaと横の長さbを入力し「長方形の面積を計算」ボタンをクリックすると、縦の長さと横の長さから長方形の面積を計算して表示します。・長方形、正方形の面積の求め方と公式の意味 ・複合図形の面積 5年 直方体や立方体の体積 ・体積の意味 ・体積の単位(㎤、㎥)と単位の相互関 係 ・直方体、立方体の体積の求め方と公 式 ・複合図形の体積 ・容積、内のりの意味 今日から図形の公式をいくつか紹介していきます。一番最初は長方形の面積の求め方からやりましょう!長方形の面積の公式は、図形の公式の中では、おそらく小学校で一番最初に習う公式だと思います。 長方形の面積の公式は、 たて×よこ です。有名な公式なので、きっと暗記している




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
えば,長方形と平行四辺形について,平行四辺形 は長方形に変形できるという関係に着目し,平行 四辺形の面積を求める式を学習する。 本教材で扱う斜角柱の体積の求め方は,小学5 年生の平行四辺形の面積を求める学習を3次元に 拡張した内容である。(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にしてたて・よこ 1cm 1 c m の正方形の面積は 1(cm2) 1 (c m 2) です。 そして正方形や長方形は 1cm2 1 c m 2 のものが『たて×よこ (個)』だけ並んでいると見ることができます。 1cm2 1 c m 2 のマスが たて・よこ に 5 5 個ずつ並んでたら全部で 5 ×5=25 5 × 5 = 25 個。



直方体の体積 表面積 体積 表面積の計算 計算サイト



Math 積み重ねた立方体の表面積 働きアリ
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru数学的な考え方 ・長方形,正方形の面積を,公式を用いて求めることができる。 技 能 ・面積について,単位と測定の意味や,長方形や正方形の面積は計算によって求められることやその 求め方を理解し,面積についての量感を身につける。 ①長方形の面積の求め方 具体的にまずは面積を求めてみましょう。 縦:3cm 横:6cm の長方形の面積は 公式の「縦×横」に当てはめると になります。 小学生のお子さんとかは 3cm+6cm=9㎠ と間違えて足し算をしてしまう子もいるかもしれません。




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット
三角柱や四角柱などの体積は、底面積 S S 、高さ h h として、次の式で求められます。平行四辺形、ひし形、長方形、正方形の違い 二等辺三角形の4つの性質と4つの条件 二等辺三角形の角度の求め方と例題 対頂角、同位角、錯角の意味を分かりやすく解説 四角形の内角の和が360°であることの2通りの証明 多角形の内角の和の公式を3通りの「テスト勉強でワークをやってるんだけど、四角柱の体積と表面積ってどうやるんだっけ?」 「とにかく、やり方をサクッと理解したい!!」 という方に向けて、 今回の記事では四角柱の体積・表面積の求め方について、 サクッと解説していきます(^^)




小5 算数 小5 3 直方体と立方体の体積 Youtube



容積 ようせき
四角錐OABCDと四角錐OEFGHは相似で、相似比はAB:EF=6:4=3:2です。 これにより、四角錐OABCDの高さは、四角錐台の高さの3倍で9cmだとわかります。 したがって、四角錐OABCDの体積は、「錐体の体積=底面積×高さ÷3」より、6×3×9÷3=54(cm 3 )です。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体長方形の面積=たて×よこ 特に問題はないですね? このあとにでてくる 平行四辺形 三角形 台形 円 これらの公式は、全てこの長方形の面積の求め方が基本となってきます。 なので、確実に覚えて



算数科予習プリント 水の体積はどうやって求めるのだろう 容積 って 何だろう 翁島 おきなしま 小学校ホームページ




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
今回は、立方体と直方体の体積の求め方(公式)について書いていきたいと思います。 立方体の体積の求め方公式 直方体の体積の求め方公式 立方体・直方体の体積を求める問題 問題① 《立方体の体積の求め方》 問題② 《立方体の体積の求め方》 問題③ 《直方体の体積の求め方そうすると、例題の直方体の場合、縦・横に 3 3 個・ 4 4 個と並べているので 1 1 段に 12 12 個。 これを 5 5 段並べているので 12× 5=60 12 × 5 = 60 個だとわかります。 1cm3 1 c m 3 が 60 60 個なので、体積は 60cm3 60 c m 3 です。
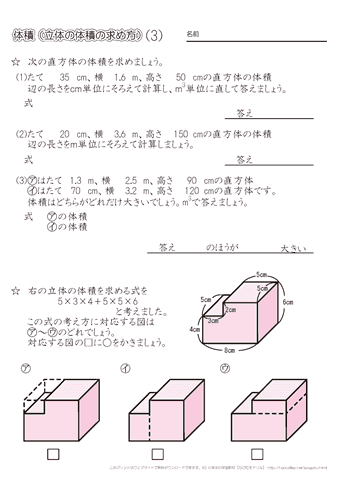



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生



5年算数体積2わかる教え方
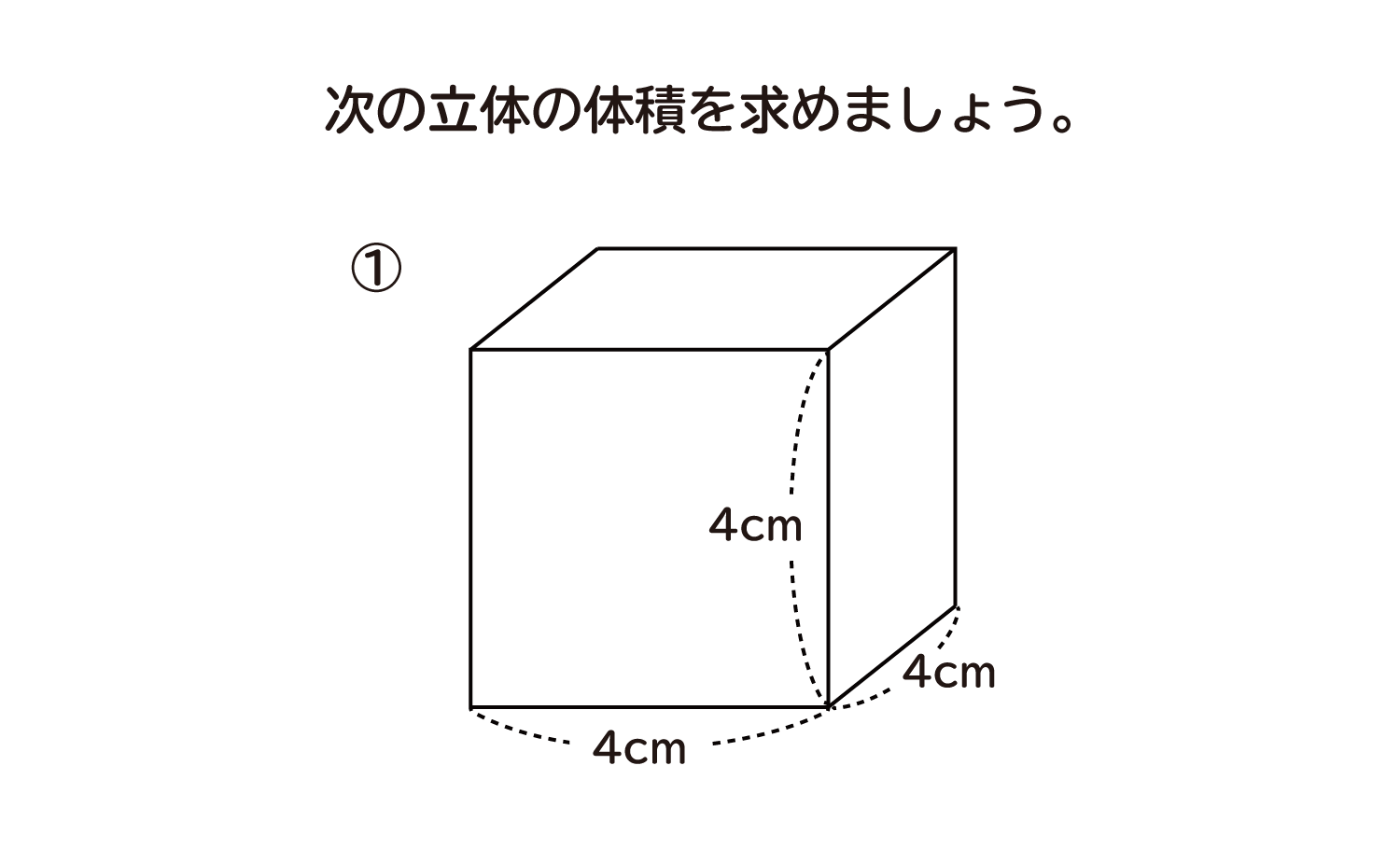



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




多くの教師が失敗する角柱の体積の求め方 算数を究める




ベスト 立方体 の 面積 ニスヌーピー 壁紙
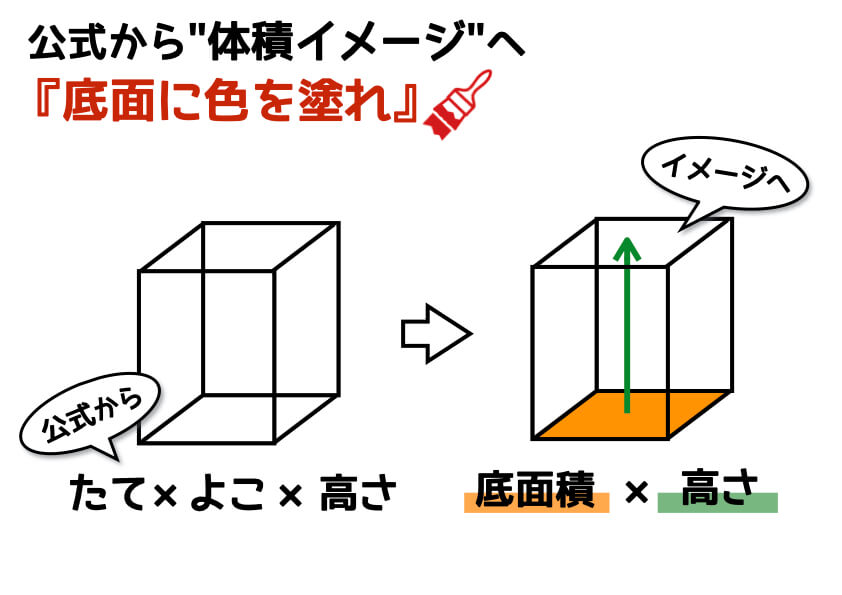



小学生でもスッキリ理解できる 体積比のコツと求め方 中学受験ナビ




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
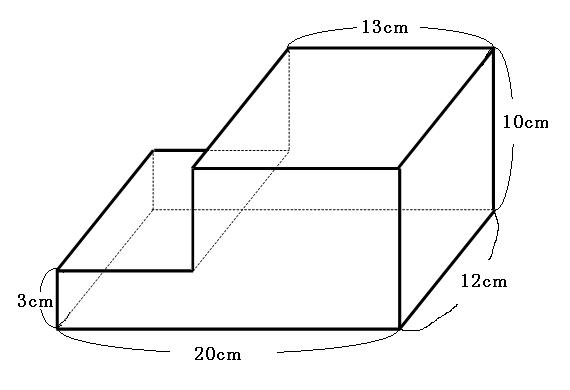



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
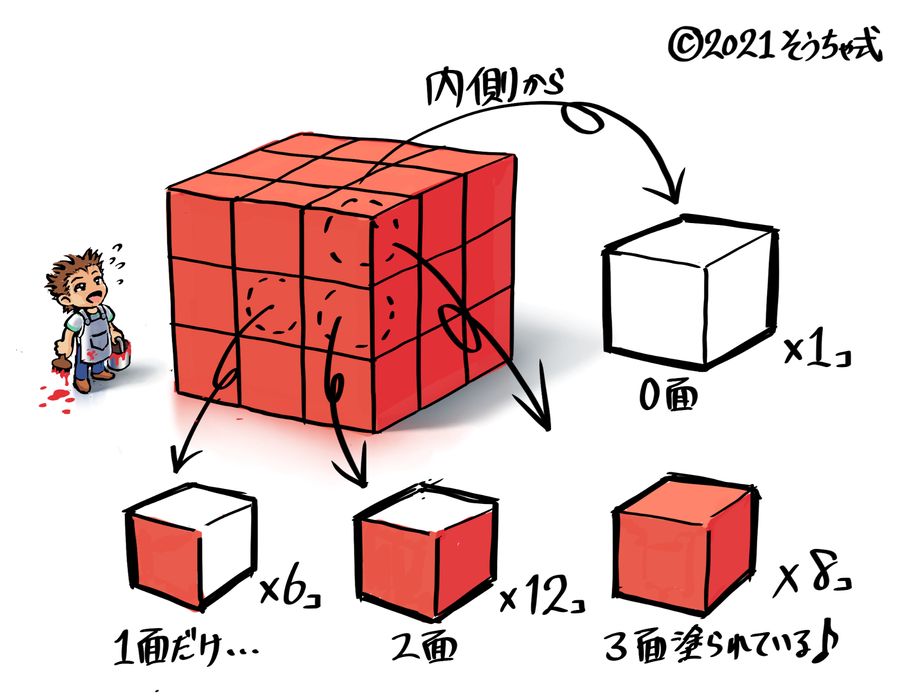



中学受験 直方体 立方体のまとめ 立体図形 そうちゃ式 受験算数 2号館 図形 速さ
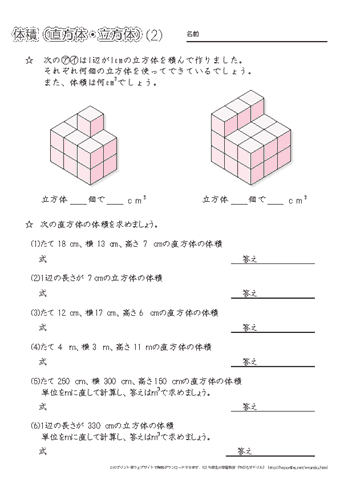



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




超簡単 体積の求め方 苦手な数学を簡単に



Www Nagoya C Ed Jp School Shimizu E 5sansu A Pdf



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
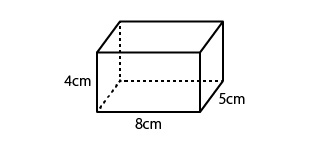



直方体の計算 もう一度やり直しの算数 数学




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー



Http Www Edu City Yokohama Lg Jp School Es Nakamaru Index Cfm 1 2687 C Html 2687 0508 Pdf



大至急 算数 数学 の質問です体積の問題だと思うのですが 縦 20 Yahoo 知恵袋
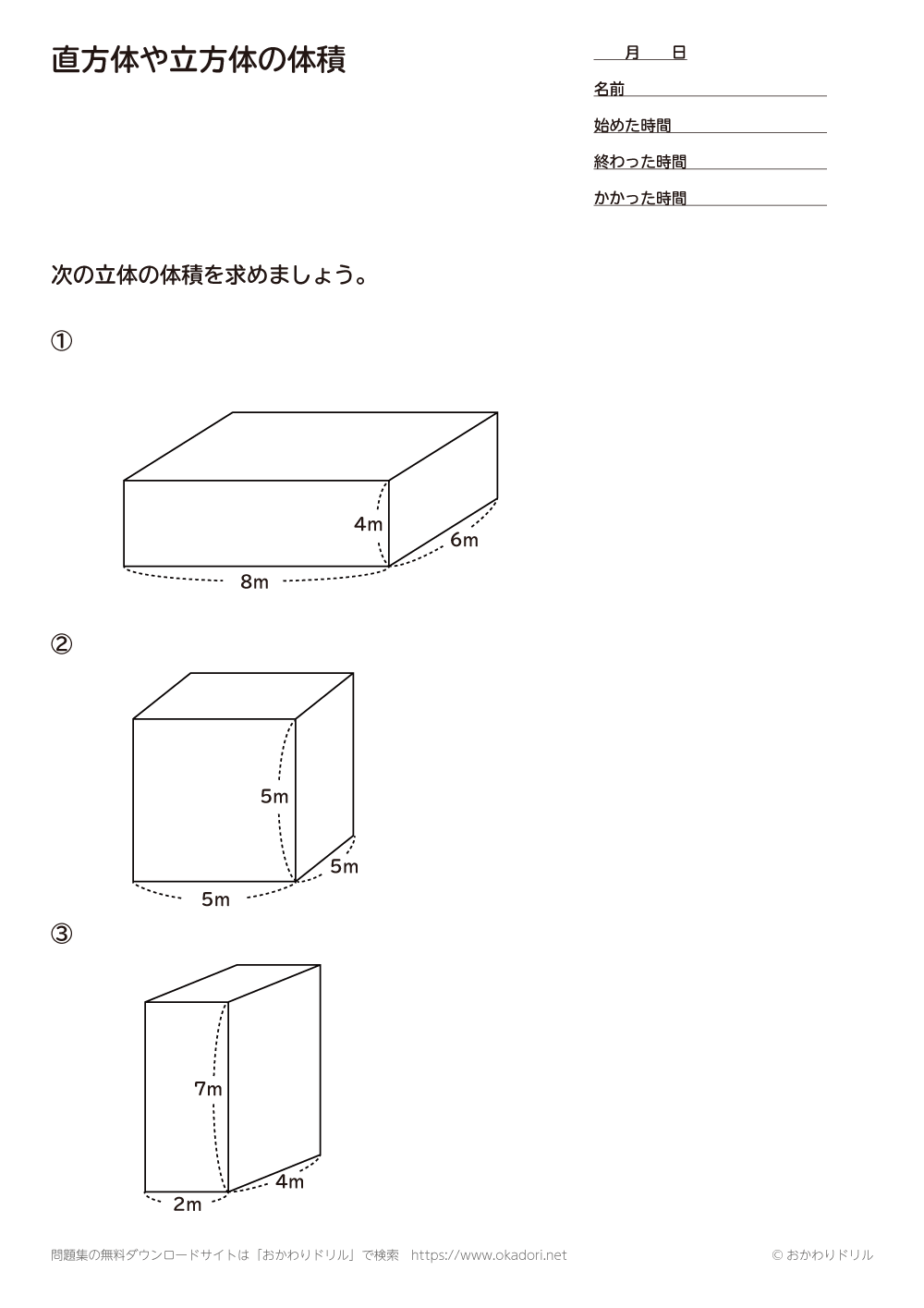



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu



1



1
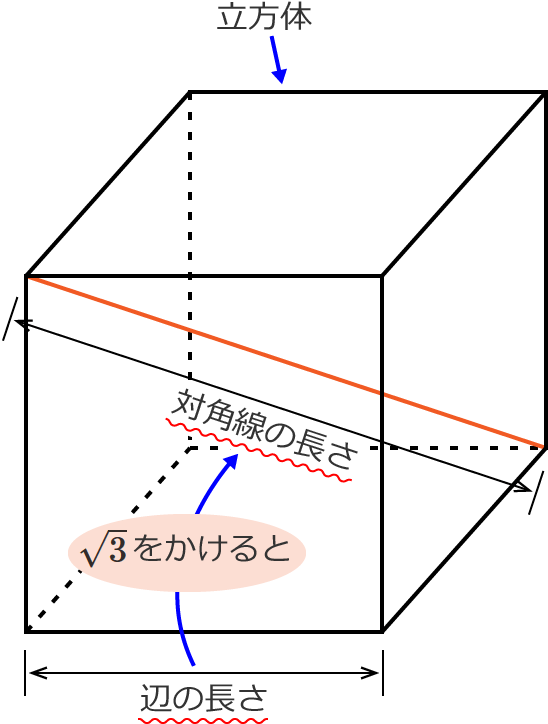



立方体の対角線の長さの求め方



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式



6年算数立体の体積1 教え方




無料印刷可能 体積 容積 求め 方




立体の体積を求める公式




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
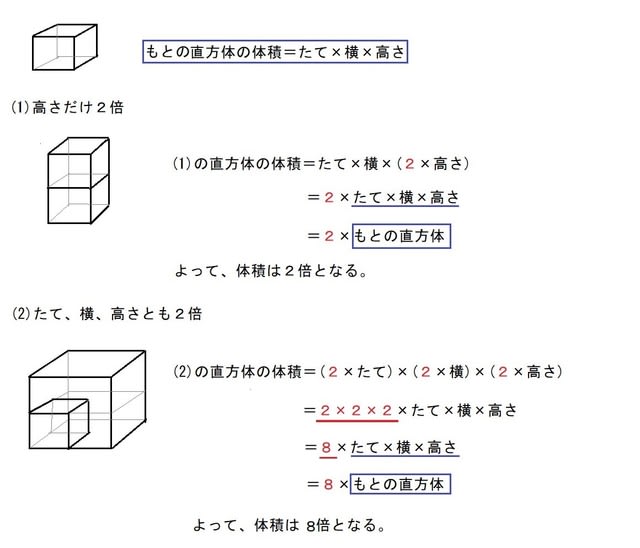



直方体 立方体の体積 小5 きちんと式を書けば簡単 算数の教え方教えますmother S Math Happy Study Support




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



5年算数体積2わかる教え方
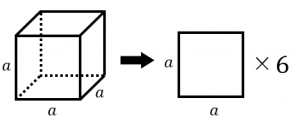



立方体と直方体の表面積を計算する 具体例で学ぶ数学




相似な直方体の表面積比 体積比 中学数学 By Okボーイ マナペディア
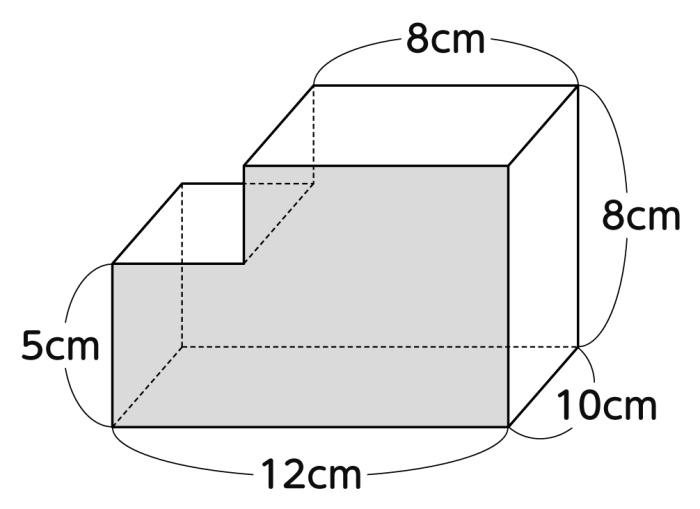



動画で学習 1 角柱と円柱の体積 算数



Www Kyoiku Metro Tokyo Lg Jp School Study Material Improvement Tokyo Basic Drill Files Math Pr05 5nen 10a Pdf




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧



1




体積 直方体 立方体 5 算数 算数 問題 算術
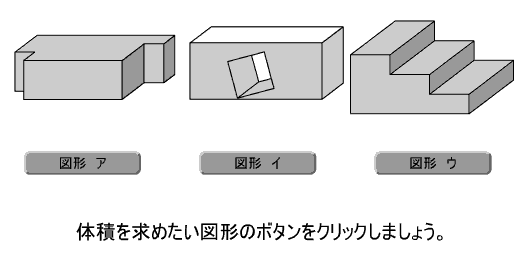



算数科5年 体積 導入 発展教材ソフトを使った授業 Note Board



Mathematics 空間図形 表面積 働きアリ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 無料学習プリント




表面積一定の円柱と直方体の体積の最大値 理系のための備忘録



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ
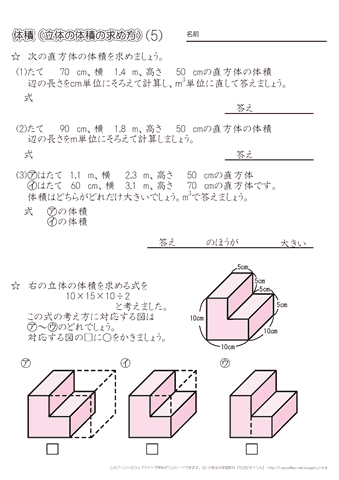



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




体積の求め方 計算公式一覧




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
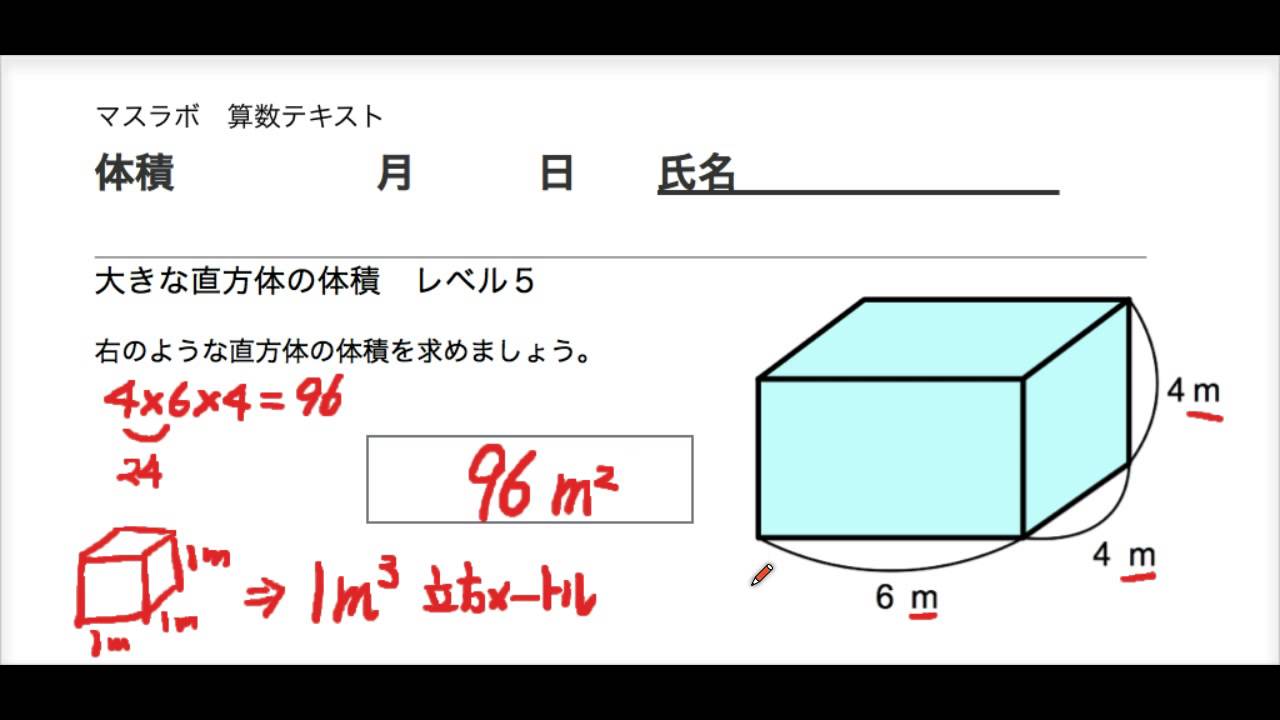



マスラボ 小学校5年 体積 レベル5 大きな直方体の体積 Youtube
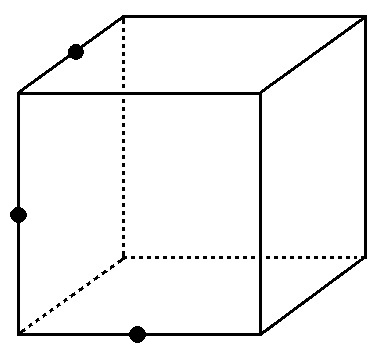



中学数学 空間図形 立体の切断問題のコツ



5 5 複雑な立体の表面積と面積を求めるには さんすうがく




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook



作成中 中学受験 容積 水の問題の解き方は 傾けたり物を沈めたり そうちゃ式 受験算数 2号館 図形 速さ




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式
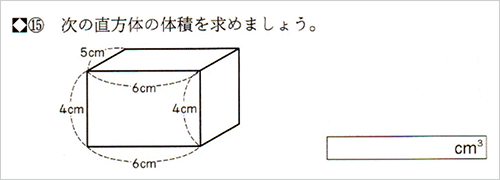



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




四角柱の体積と表面積の求め方




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




四角錐台の体積 高精度計算サイト



中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
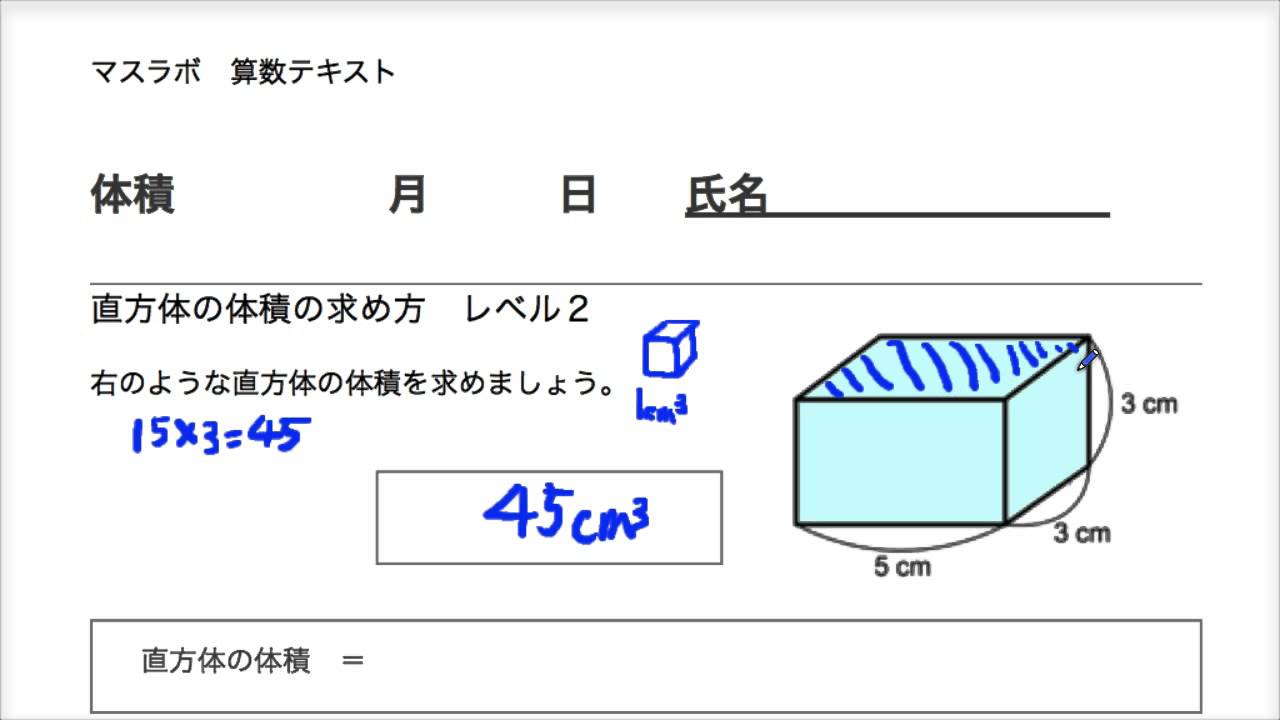



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



Search Results For Page 312 横山験也のちょっと一休み



立体の体積は平行線でね 基本に忠実に本質を伝える 楽天ブログ



1




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張



地図の体積計測




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




どうして1 3なの 錐の体積の公式の求め方 まなべーと
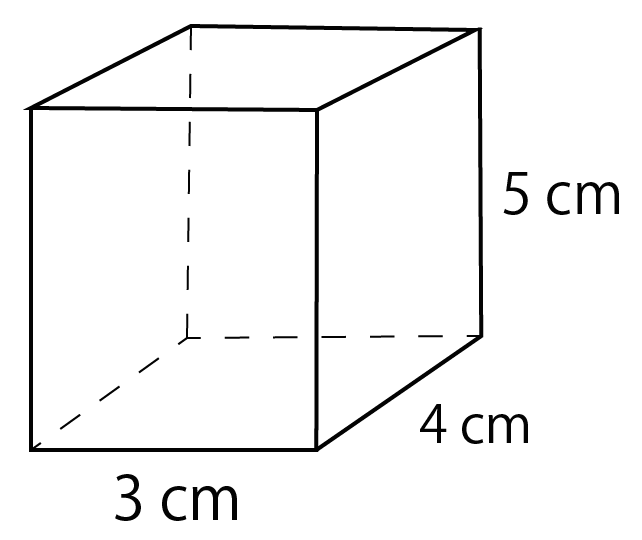



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧
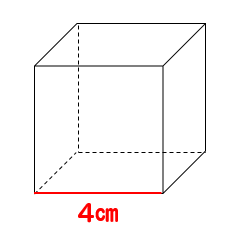



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ




小5 算数 小5 5 体積の求め方のくふう Youtube
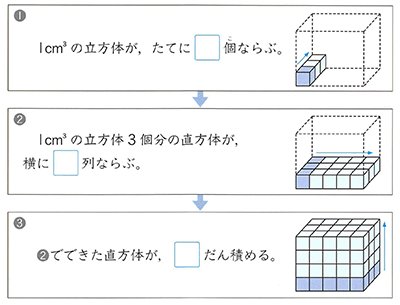



Kistenkasten723 5年生は どうして 直方体の体積が縦 奥行 横 幅 高さという公式で求められるかを学習しています 単元テストは 入試や検定試験などと違い 授業の一環であり 授業でやったことができるかどうかを確認するのが目的です



Http Www1 Iwate Ed Jp Tantou Kyouka Seika Katuyou Q Math Elementary Question Math Elementary Q 02 Pdf
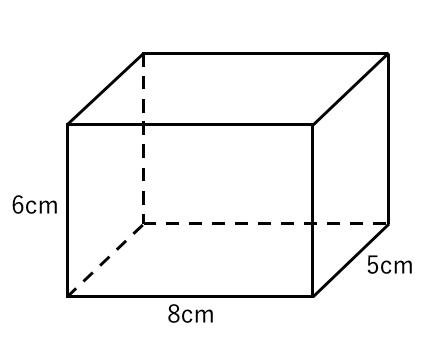



立体の体積を求める 苦手な数学を簡単に



直方体 の 体積 の 求め 方 公式



Www City Hadano Kanagawa Jp Www Contents Simple Kuukan291 Pdf



0 件のコメント:
コメントを投稿